Balloons are intimately connect to competitive programming. On
contests such as MIUP, for each problem solved you get a balloon with
the color associated to the respective problem. After the closing
ceremony, it is a tradition to just let the balloons go and fly. Some
of the balloons get stuck on some parts of the ceiling, others blow up
on spiky surfaces and others just wander into the open air. We need to
predict the trajectory of each balloon.
Balloons are filled up with helium and will always fly up in a straight vertical line, unless they encounter some obstacle. You are given a 2D view of the part of the world you need to consider. For simplification, the balloon may be considered as a single point with almost negligible size. Obstacles are given as line segments and may be of two types: spiky and normal. When a balloon touches a spiky obstacle, it immediately blows up regardless of its slope. When it encounters a normal obstacle, it may do one of two things. If the obstacle is an horizontal line it will get stuck on it. If it has a slope, no matter how small it is, it will continue flying, turning to the right or to the left depending on the angle of the slope.
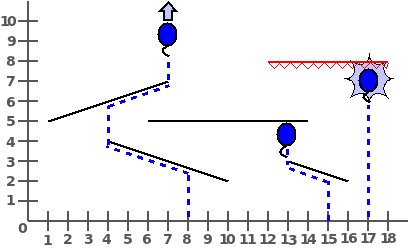
The following figure illustrates an example world with five obstacles (one of them is spiky), and what would happen with three different ground locations, given by the X coordinate. The balloon launched on X=8 will fly into the open space after touching two obstacles. The balloon of X=15 will get stuck on the 2nd obstacle it encounters. Finally, the balloon launched on X=17 will be blown up on the first obstacle it will collide with, because the obstacle is spiky.
Given a set of L line segments, identified by its endpoints, and a set of N balloon ground launch coordinates, your task is to compute the trajectory of all the balloons, identifying whether they will wander into the open space, get stuck or get blown up. You must also calculate how many obstacles they will collide with, before fulfilling their destiny.
The first line contains a single integer L, indicating the number of line segments. Then follow exactly L lines, each one in the form X1i Y1i X2i Y2i C, describing the i-th line segment. Each line segment has its endpoints at the integer coordinates (X1i,Y1i) and (X2i,Y2i) and C is a single character, being ’N’ if the line segment is normal, and ’S’ if it is spiky. Both the segments and their endpoints can be in any order.
After this comes a single integer N, indicating the number of balloons to consider. Then come N lines, each one with a single integer Bi indicating the X coordinate of the i-th balloon. You can assume that all balloons will be launched at ground level, that is, with Y=0.
You can also assume that no two X coordinates will be the same, regardless of being from an endpoint or a balloon, and that there are no intersections between line segments.
The output should be composed of N lines, one line per balloon in the same order they appeared in the input, saying what happened to each balloon. Each line may be of one of the following three types:
| 1 ≤ L ≤ 100 | Number of line segments |
| 1 ≤ X1i, Y1i, X2i, Y2i ≤ 40,000 | Coordinates of line segment endpoints |
| 1 ≤ N ≤ 100 | Number of balloons |
| 1 ≤ Bi ≤ 40,000 | X Coordinates of balloon launching points |
5 4 4 10 2 N 16 2 13 3 N 6 5 14 5 N 12 8 18 8 S 7 7 1 5 N 6 8 15 17 19 2 11
fly 2 stuck 2 blow 1 fly 0 fly 1 stuck 1
Explanation: The line segments of the sample input, and the first three balloons, are the ones depicted in the given figure. The balloon launched on X=19 flies away without touching any object. The balloon launched on X=2 touches one obstacle and then flies away. Finally, the balloon of X=11 gets stuck on the first segment it encounters, which is horizontal.
MIUP'2012, 20 de Outubro, DCC/FCUP
This document was translated from LATEX by HEVEA.