Problema F

Autor: André Restigo (Faculdade de Engenharia da Universidade do Porto)
Tipo de problema: Grids + Programação Dinâmica
Número de ficheiros de teste: 20

Este era um problema interessante e que acabou por ser o único que não foi resolvido por nenhuma equipa. Essencialmente pedia-nos para descobrir qual o tamanho mínimo dos retângulos que formavam a "grelha" completa.

Essencialmente, a nossa tarefa podia ser dividida em duas partes:

Descobrir quais as linhas (e colunas) que eram candidatas a ser "linhas divisoras" (ou seja, que não "cortavam" a meio uma "tile" da mesma cor;
Sabendo as linhas divisoras, descobrir os menores múltiplos que as podiam "explicar".

Comecemos pela primeira parte:

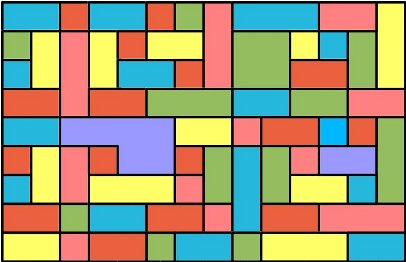
Seja N o número máximo de de linhas e/ou colunas. Se considerarmos apenas o eixo horizontal, temos exactamente (N+1) posições candidatas a "linhas divisoras". Podemos passar por cada uma delas e depois descer em cada uma dessas posições as N linhas e verificar se nalguma posição a linha dividiria uma tile da mesma cor. Algo muito semelhante pode ser feito depois no eixo vertical, resultando num método com complexidade O(N^2) para descobrir as "linhas divisoras", em ambos os eixos.

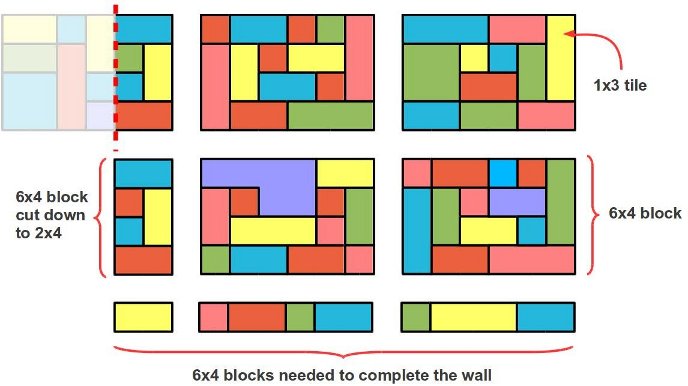
Depois disto, resta a segunda parte do problema. A primeira coisa a notar é que a largura do menor retângulo é independente da sua altura. Dito de outro modo, podemos primeiro encontrar o menor múltiplo que explica as linhas divisoras encontradas no eixo horizontal, e depois fazer o mesmo para o eixo vertical.

Mas o que que é realmente encontrar o menor múltiplo que explica as linhas divisoras? Encontrar as linhas divisoras vai-nos dar um conjunto de números (ex: {1, 2, 5, 7, 10}. O que queremos é encontrar o menor número M tal que:

Existe uma posição inicial P₁ que está situada numa posição menor ou igual a M (próximo da borda a "tile" maior pode estar cortada).
Todas as posições P₁+K*M até uma posição a distância menor ou igual a M da borda final são linhas divisoras (ou seja, os múltiplos de M a seguir à posição inicial confirmam a "hipótese" de M ser o tamanho menor que "explica" as linhas divisoras).

Falta perceber como encontrar este número M. A hipótese mais exaustiva seria para todas as posições iniciais (no máximo N), tentar todos os múltiplos M possíveis (no máximo são N) e a partir daí iterar sobre as posições múltiplas a partir da inicial (no máximo N). Isto tudo daria um algoritmo cúbico O(N^3) que não passaria no tempo (embora se possam fazer muitos cortes).

Como resolver isto em tempo quadrático? Uma hipótese é usar programação dinâmica (PD). Consideremos o seguinte (existiam outras formulações possíveis):


can[M][i] = Posso chegar à posição i com o múltiplo M

Para um dado M, podemos fazer o seguinte:


- Para i entre 1 e N, can[M][i]=False [inicializar todas as posições a false]
- Para i entre 1 e M, se linhadivisora[i], então can[M][i]=True [junto à borda]
- Para i entre 0 e N-M, se can[M][i] e linhadivisora[i+M], então can[M][i+M]=True [múltiplos]
- Para i entre N-M e M, se can[M][i]==True, então posso escolher o múltiplo M [junto à borda]
- Caso a alínea anterior não se verifique, não posso usar esse M.

Cada M tem então uma maneira linear - O(N) - de ser verificado, e como temos no máximo N possíveis múltiplos, ficamos com um processo final de complexidade quadrática - O(N^2) - que passava no tempo!

Ligações interessantes:

Problema F - Tiled Wall