

|
Problema I - Flying Balloons |
 Autor: Pedro Ribeiro (Faculdade de Ciências da Universidade do Porto)
Autor: Pedro Ribeiro (Faculdade de Ciências da Universidade do Porto)
Tipo de problema: Geometria, Simulação, Intersecção de Linhas
Número de ficheiros de teste: 12
Neste problemas tínhamos de descobrir o percurso de um balão quando lançado para o ar.
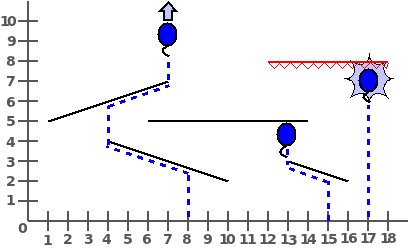
O problema base subjacente é, dada uma posição qualquer, se traçarmos uma linha vertical a começar nesse ponto, saber qual o primeiro segmento de recta que essa linha vai intersectar. Chamemos a este segmento de recta next_intersect(x,y)
Sabendo isto, resolver o problema é simplesmente começar por chamar next_intersect(x,0) e depois ao chegar a um segmento:
A parte fulcral é portanto saber implementar next_intersect().
Para simplificar este problema, é garantido que não existem interseccoes entre segmentos e que não existem coincidências nas coordenadas do eixo dos X. Isto ajuda a evitar casos degenerados, sempre complicados para algoritmos geométricos. Isto significa também que não existem segmentos verticais e que por isso até podemos usar a "clássica" equação y = mx + b.
Como temos dois pontos da recta, conseguimos calcular m e b. Sabendo isto e sabendo o x onde estamos, conseguimos calcular o ponto de intersecção com a linha e perceber se está dentro do segmento dado (notem que não chegaria ordenar os segmentos pelo extremo inferior).
Tendo em conta os limites dados (100 segmentos) podiamos exaustivamente testar sempre todos os segmentos como possíveis candidatos para a próxima interseção. Era possível fazer melhor com algum tipo de "organização espacial" (por exemplo ordenar os pontos por Y e "varrê-los" nessa ordem), mas em concurso devem seguir o princípio KISS e implementar o algoritmo mais "simples" que funcione para os limites dados.
Ligações interessantes: